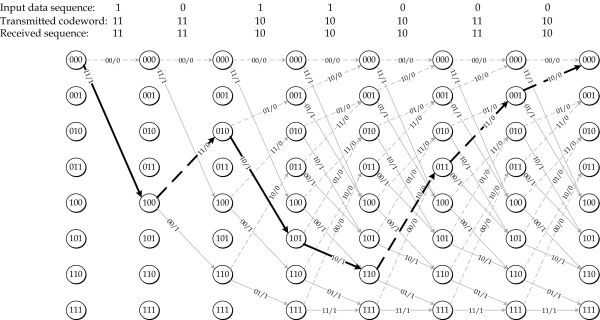
Introduction

Tailbiting convolutional codes (TBCC) are widely used (PDCCH LTE, 802.11), because they:

• Can be represented as quasi-cyclic block codes.
• Have equal error protection over all bits if we compare with truncated construction.
• Achieve the best minimum distance for short- and medium lengths.
• Allow easy rate matching.

The main drawback of TBCC is an additional decoding complexity. Decoder (e.g. Viterbi) shall know/predict the starting state in a trellis. In this series of posts I will provide an overview of main existing methods/ideas and patents.

Notation

The following notation will be used

• \(m\) - constraints length
• \(R = \frac{K}{N}\) - rate
• \(K\) - number of shift registers used (let’s assume we use controller canonical form)

Note: “Controller canonical form” has encoder implementation with \(K\) registers and \(N\) adders. The other known form is “Observer canonical form”. It is done with \(N\) shift registers and \(K\) adders.

Reference Decoder

Well, as the reference decoder we will use Viterbi decoder, that starts on every possible starting state. The decoding result is a closest codeword sequence over all possible runs.

Total required Viterbi runs is \(2^{mK}\)

Classification

Simply, all methods can be divided into following groups: 1) Suboptimal - tries to reduce space of possible starting states 2) …

(1986) Article “On Tail Biting Convolutional Codes” by H. MA, J. Wolf

Source on IEEE DOI: 10.1109/TCOM.1986.1096498

This article compares solution from Bard-David with author’s one.

Bard-David (1982) - suboptimal

Algorithm offers custom steps order and has following steps:

1. Choose an arbitrary starting state and Decode using a maximum likelihood decoder.
2. Check if the starting state is the same as the ending state. If yes, stop, otherwise go to step 3.
3. Use the previous ending state as the new starting state.

Two-step scheme - suboptimal

Author (H.Ma) provides own steps order, based on continued fractions list. The algorithm does the following:

1. Obtain ordered list of \(2^{mK}\) starting state using an algebraic method called “continued fractions”. The method is described in PhD and, unfortunately,not available
2. Run with starting state from list until found

US 6256764 (2001) - suboptimal

Author: Atallah Isa Bisher Pattent 6256764 Algorithm:

1. set all starting states scores to 0
2. Run viterbi
3. find ending best state \(S_min\)
4. find set of other passes \(\beta = {S_i}: dist(S_i, S_min) < K\)
5. Find state in \(\beta\) set, where starting state and ending state is the same

References

1. H. Ma and J. Wolf, “On Tail Biting Convolutional Codes,” IEEE Trans. Commun., vol. 34, no. 2, pp. 104–111, Feb. 1986, doi: 10.1109/TCOM.1986.1096498.
2. R. Y. Shao, Shu Lin, and M. P. C. Fossorier, “Two decoding algorithms for tailbiting codes,” IEEE Trans. Commun., vol. 51, no. 10, pp. 1658–1665, Oct. 2003, doi: 10.1109/TCOMM.2003.818084.

Last update:29 November 2020