Introduction

The Hidden Markov Models is an extremely powerful subclass of probabilistic temporal models. The concept of using hidden(latent) variables and estimation of their values is used in various algorithms, like Kalman filters, and in many applications, like speech recognition or turbo codes decoding.

It seems that artificial recurrent neural networks (RNN) and a concept of Long short-term memory (LSTM) assimilate the nature of Hidden Markov Models by combining hidden (latent) variables within a deep neural network.

I was always excited how powerful HMMs could be and what elegant solutions they could bring. By the next series of post, I would like to provide a few examples, how HMMs used in some selected algorithms and applications.

Simplest example

Assume that we have a temporal graphical model that produces step by step some samples from states S and O. “S” samples are hidden (latent) and are staying unknown for us. “O” samples are observed. For every sample “S” there is a corresponding sample “O”.

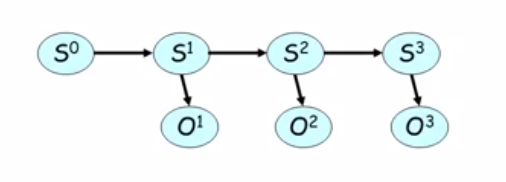
The simplest example of HMMs is a speech recognition task. Imagine that a person said some word. The word consists of letters. Some letters are inaudible. Some letters were pronounced unclearly. Some letters sound similar to others. But our brain can use some prior knowledge and can determine the original word.

Simple, right? We just wanted to estimate “S”s using “O”s. But can we imagine some extra applications? Yes, we can do something more exciting.

It is clear, that estimation of “S” depends not only on samples “O”, but depends on our prior knowledge. Let’s call this prior knowledge as a model.

Can we find the model, that gives us the best “S” for a given “O”? Yes! And Expected Maximization(EM) algorithm does it. Now, we can train a model using known “S” and “O”.

Can we have some more fun? Yes. We may notice, that for the same observations different models provide different estimations of “S”. It means, that a model defines a transformation of data to other data. And it automatically brings us the understanding how generative networks work.

Ok, no more words. Let’s dive deep.

Hidden Markov Models

The best resource to start with HMMs is the article of L.A. Rabiner “A tutorial on hidden Markov models and selected applications in speech recognition”.

We will use the same notation as in the article of L.A.Rabiner, namely:

Possible states: \(S = {S_1, S_2...S_N}\)

Possible observations: \(O = {O_1, O_2, ... O_M}\)

Our Model: \(\lambda = (A, B, \pi)\), where:

1. \(A_{ij} = P(S_j \mid S_i)\) - state transition probability distribution.

2. \(B_{ij} = P(O_j \mid S_i)\) - observation symbol probability distribution.

3. \(\pi = \{P(S_1^{(1)}), P(S_2^{(1)}) ... P(S_N^{(1)}\}\) - initial state distribution.

We can have three main problems

Problem 1: Direct computations

Q: How do we compute the probability that the observed sequence was produced?

In other words: if we observe \(\hat{O} = \{\hat{O_1},\hat{O_2}...\hat{O_L}\}\), what is \(P(\hat{O} \mid \lambda)\) ?

A: First step of Forward Backward Algorithm

Problem 2: Hidden states estimation

Q: What is sequence \(\hat{S} = \hat{S_1},\hat{S_2}...\hat{S_L}\) that could “most likely” produce our sequence \(\hat{O}\)?

By “Most likely” we can use different criteria: Maximum Likelihood or Maximum a posteriori probability.

A: Full Forward Backward Algorithm

Problem 3: HMM training

Q: How can we train a model so to best describe how given observation sequence comes about?

In other words, we may use “observation sequences” to adjust parameters of the HMM ( do “training”) to get the best model for real phenomena

A: EM algorithm (Expected Maximization Algorithm)

References

1. L. R. Rabiner, “A tutorial on hidden Markov models and selected applications in speech recognition,” Proc. IEEE, vol. 77, no. 2, pp. 257–286, Feb. 1989, doi: 10.1109/5.18626.
2. Probabilistic Graphical Models 1: Representation, Temporal Models - HMMs
3. Николенко, “Лекция 9. Скрытые марковские цепи”

Last update:15 May 2021